2021下半年软件设计师考点分析:图
- 时间:2021-08-06 12:38:45
- 原文
摘要:很多考生在备考2021下半年软件设计师考试,小编为大家整理了软考中级软件设计师考点分析:图,供大家备考复习。
【考法分析】
本知识点的主要考查形式有:判断给出的关于图的概念、特性的描述是否正确;或根据图的邻接矩阵、邻接表,指出相关图、图的特点、图的遍历;根据图示,指出遍历顺序、拓扑序列。
【要点分析】
1、完全图
在无向图中,若每对顶点之间都有一条边相连,则称该图为完全图(complete graph)。
在有向图中,若每对顶点之间都有二条有向边相互连接,则称该图为完全图。
2、图的邻接矩阵表示:用一个n阶方阵R来存放图中各结点的关联信息,其矩阵元素Rij定义为:
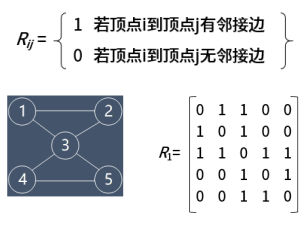
3、图的邻接表表示:首先把每个顶点的邻接顶点用链表示出来,然后用一个一维数组来顺序存储上面每个链表的头指针。
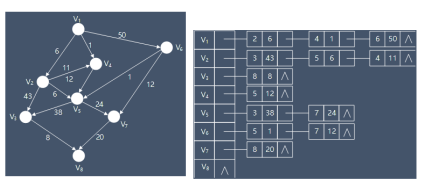
4、图的遍历:
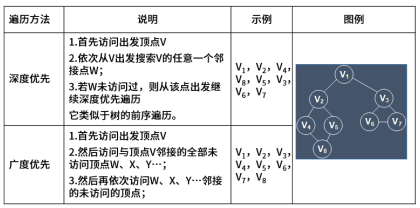
5、图的拓扑排序:拓扑排序是将AOV网中的所有顶点排成一个线性序列的过程,并且该序列满足:若在AOV网点中从顶点Vi到Vj有一条路径,则在该线性序列中,顶点Vi必然在顶点Vj之前。
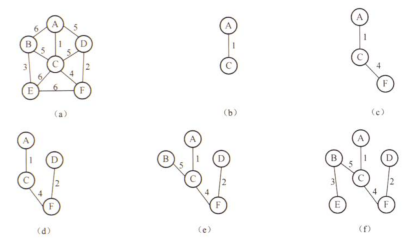
6、最小生成树,是该图的极小联通子图。普里姆算法构造最小生成树过程:
(1)去掉所有的连线,将所有顶点放到集合R1中,作为未处理结点集合,另新建集合R2存放已处理结点。
(2)选择入度为0的顶点作为起点,放到集合R2中;
(3)选择R2到R1最短(代价最小)的路径,同时将对应顶点从R1删除并放到集合R2中。
(4)重复步骤3直到R1为空。
【备考点拨】
1、掌握图的相关概念;
2、掌握图的存储;
3、掌握图的遍历;
4、掌握图的拓扑序列求取;
5、了解最小生成树的构造。